6.3.1. Filtre passe-bas¶

Un filtre passe-bas est un filtre qui laisse passer les basses fréquences et atténue les hautes fréquences.

6.3.1.1. Fonction de transfert du premier ordre¶

Un filtre du premier ordre est défini par la fonction de transfert suivante : \(H(jw) = \frac{ signal\ de\ sortie}{signal\ d'entrée } = \frac{ K }{ 1 + j\ \frac { w }{ w_c } }\)

Son module vaut : \(\left| H(jw) \right| = \frac { K }{ \sqrt{ 1 + (\frac { w }{ w_c })^2 }}\)

Son argument vaut : \(\phi (w) = arg(H(jw)) = -arg(1 + j \frac{w}{w_c}) = -arctan(\frac{w}{w_c})\)

6.3.1.2. Filtre RC passif¶

Un filtre RC est un circuit passif à base de résistance et de condensateur.

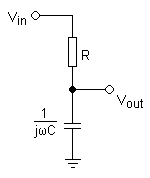
../_images/passe_bas_passif_composants.png

Sa fonction de transfert vaut : \(H(jw) = \frac{ signal\ de\ sortie}{signal\ d'entrée } = \frac{ K }{ 1 + jRCw }\)

Sa fréquence de coupure est : \(f_c = \frac{1}{2\pi RC}\ ou\ w_c = \frac{1}{RC}\)

Son gain en décibels vaut : \(G_dB(w) = 20 \log {K} - 10 \log ({1+(wRC)^2})\)

Sa phase en radians vaut : \(\phi (w) = -arctan(wRC)\)

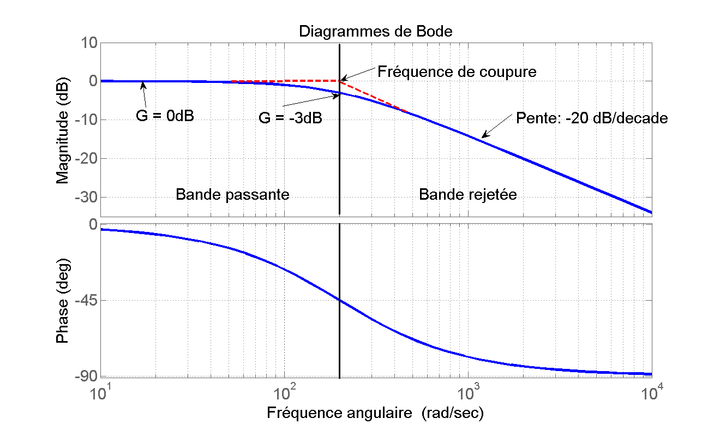
Si \(w \ll w_c \ :\ G_dB \approx 0\ et\ \phi \approx 0\) => filtre passant

Si \(w \gg w_c \ :\ G_dB \approx -20 \log {\frac {w}{w_c}}\ et\ \phi \approx -90\) => signal filtré

Si \(w=w_c \ :\ G_dB = -3\ dB\)

6.3.1.3. Filtre actif¶

Un filtre actif permet d’augmenter le gain dans la bande passante.

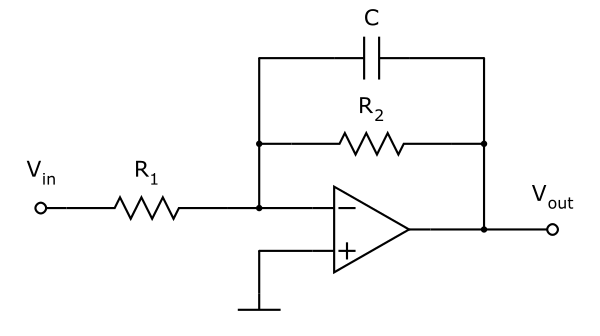
../_images/passe_bas_actif_composants.png

Sa fréquence de coupure est : \(\frac {1}{2 \pi R_2 C}\ ou\ w_c = \frac{1}{R_2 C}\)

Sa fonction de transfert est : \(H(jw) = \frac {-R_2}{R_1} * \frac{1}{1+jR_2 Cw}\)

Si \(w \ll w_c \ :\ H(w) \approx \frac {-R_2}{R_1}\)

Si \(w \gg w_c \ :\ H(w) \approx 0\)